でたらめな命題
科学研究方面で、近年青年同志の、活躍がめざましい。彼らの研究の突出する特長は、“敢想敢説敢干”[自由な発想、積極発言、失敗を恐れない]であることだ。しかし、これが原因でしばしば一部の人から批判され、彼らの科学研究論文が、「でたらめ」と貶されることがある。ほんとうに、でたらめかどうかは、慎重に検討されねばならない。
エンゲルスは『自然弁証法』において、自然科学のかずかずの旧命題を激しく批判し、形而上学の誤りを指摘して、唯物弁証法の観点から果断に新しい研究を行うべきことを提唱した。例えば、数学の研究では、でたらめとこき下ろされた命題を支持する側にまわり、このように書いている。
“高等数学では、初等数学における永遠の真理を、既に克服された観点とみなし、相反する判断を下す。それは、初等数学の代表人物からみれば、このうえないでたらめな命題である。固定された範疇はここでは消滅する。数学がこのような領域に進めば、簡単な関係、例えば抽象的な量的関係、無限大について、弁証方式が採用されるので、数学者は、自覚するしないに拘わらず、好む好まざるに拘わらず、いつのまにか弁証法的数学者になっているのである。”

多くの事例が証明するごとく、科学史上においては、エンゲルスのこの論断は実に正確だ。高等数学の命題が提出された当初、初等数学界からはでたらめな説とたたかれた。数学のみならず、その他の科学命題においても、新説が提出されるたびに、でたらめな代物とこき下ろされたではないか?
初等数学の知識しかなかった頃は、静止的固定常数のみが計算可能で、これを以て客観事物の量的関係を表した。高等数学が現れると、発展運動中の変数をも計算できるようになった。初等数学は機械論的形而上学の観点からの支配を受け、唯物弁証法の観点が欠如し、初等数学知識しか持ち合わさない人は、どうしても事物の弁証関係を正確に理解することができなかった。例えば、曲線と直線の関係であるが、初等数学を主張する側から見れば、それは絶対に異なる二つの概念であり、曲線を無限に延長させると、直線になるとは考え及ばないことであった。高等数学の微分においては、曲線と直線が等しい。このように、初等数学の代表人物の見方では、高等数学の多くは、当然全くでたらめな命題となる。

同じ例はその他学科の中においても少なからず存在する。例えば、カモノハシをどう分類するか動物学者は知らなかった。帰納法で動物を分類すると、雌で乳房のある動物は全て哺乳類の動物に数えられ、反対にあらゆる動物の雌で乳房のない動物は哺乳動物として扱われなかった。この標準で見ると、カモノハシは、当然哺乳類動物でない。雌のカモノハシは乳房がないからである。しかし、カモノハシは完全な哺乳類であることは、事実が証明している。それで、帰納法で動物を分類すれば、当然過ちを犯すことになる、とエンゲルスは指摘する。
これにより明らかなように、分野を問わず、科学の定説は永遠不変と見るべきでなく、また同様に科学的新説は、そこに理が成立すれば、これに故有りとし、でたらめであるとして片付けるべきではない。
客観的法則は、数多の反復経験を通して始めてそれが明らかになる。科学研究の命題と結論は人間の客観的法則に対する一種の認識段階にすぎない。昨日正確であった結論が、翌日には新事実の証明により、完全無欠でなくなる。この時、元来の結論に対して修正と補充が必要となるか、新しい結論が出される。このように、人間の認識は不断に発展向上し、科学研究はさらに合理的に客観法則を手中に収め、人類に奉仕することが出来る。
科学研究が豊かな成果を得るために、我々は若い人たちの大胆な研究、思想の解放、“敢想敢説敢干”[自由な発想、積極発言、失敗を恐れない]を、もろ手を挙げて奨励するべきで、彼らに冷水を浴びせ、やる気をそぐようなことをしてはならない。我々は積極的に若い科学技術者や基礎科学研究者を啓発して、着実に、虚心坦懐に科学の高峰に向かって前進させねばならない。みなさんも勉励これ勤め、焦って軽薄に走ってはいけない、またでたらめと批判されるのに恐れをなして自己の向かう道を放棄してはならない。反対から言えば、誰でも着実な基礎研究の上に、真の新しい発見があれば、いわゆるでたらめな新しい命題を、勇気を出して提出すべきであり、なんら躊躇することはない。
【 掲載当時の時代考証と秘められたメッセージ 】
「胡説八道」的命題 ひとそえ
題目にも、本文のなかにも「胡説八道」の四文字がたびたび使われている。「胡説八道」をどのような日本語にするかについては、長い時間をかけて考えました。拙い経験乍らこの言葉には口語的な印象があり「胡説!」と合いの手のように発せられると「そんなアホな!」という印象を持ちました、ということで漢語四文字熟語の「荒唐無稽」ではなく「でたらめ」という日本語にさせてもらいました。
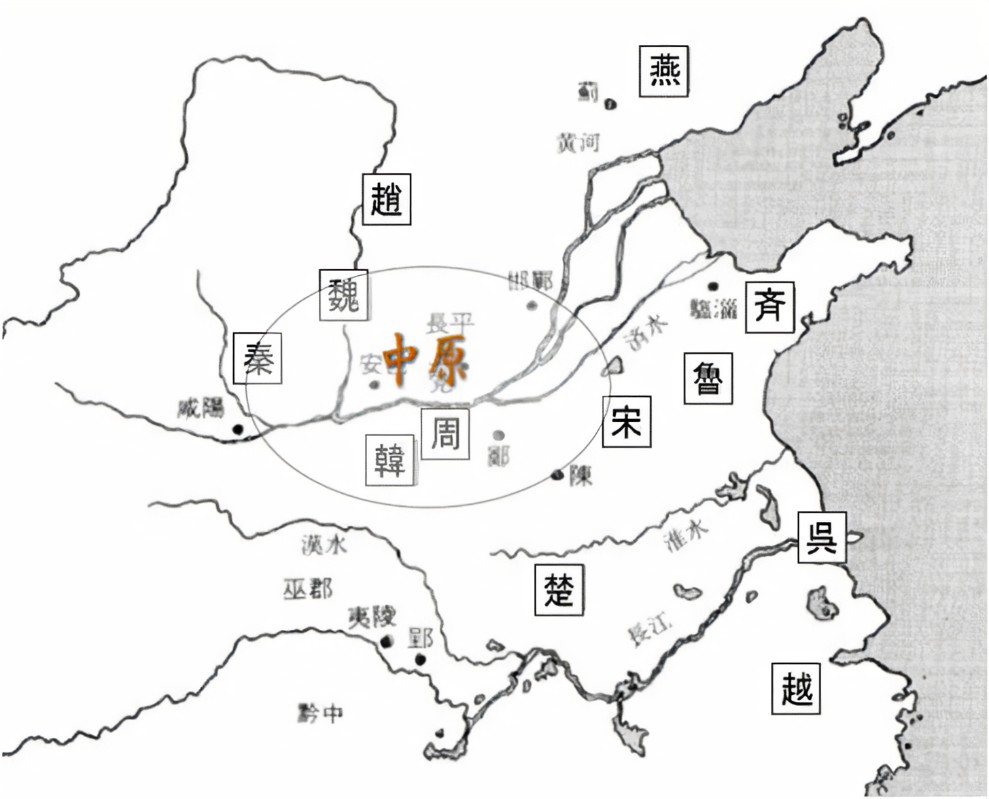
自分たちに耳慣れない言葉には違和感どころか嫌悪感まで持つ場合があります。しかも中華中原の人にとって辺境の言葉には「何をいっているのか?」「違和感」「でたらめ」という排除の感情を持ったのではないかと想像します。 この文章の核は「昨日正確であった結論が、翌日には新事実の証明により、完全無欠でなくなる。この時、元来の結論に対して改良と補充が必要となるか、新しい結論が出される。このように、人間の認識は不断に発展向上し、科学研究はさらに合理的に客観法則を手中に収め、人類に奉仕することが出来る。」の一節であり、毛沢東が完全無欠とされた神話が崩れかかった時代背景に注目しました。併せて根強い完全無欠の神話造りの動きにも注視していかねばなりません。
文・井上邦久
“胡说八道”的命題 原文
我们的青年同志,近年来在从事科学研究中,做出了很大的成绩。他们的研究工作最突出的特点是敢想敢说敢干。但是,他们也常常因此而受到一些人的责难,他们的科学研究文章也有的竟然被批评为“胡说八道”。到底是不是胡说八道呢?这是需要仔细分析的问题。
恩格斯在《自然辨证法》中,曾经尖锐地批评了许多自然科学的旧命题,指出它们的形而上学的错误,而提倡要敢于用唯物辩证的观点进行新的研究。比如,恩格斯对于数学的研究工作,就特别支持那些被看成是胡说八道的命题。恩格斯写道:
“高等数学把初等数学的永恒真理看做一个已被克服了的观点,常常做出相反的判断,提出一些在初等数学的代表人物看来是完全胡说八道的命题。固定的范畴在这里消失了。数学走到了这样一个领域,在那里即使很简单的关系,如抽象的量的关系,恶的无限,都采取了完全辩证的形式,迫使数学家们既不自觉又不自愿地转变为辩证的数学家。”
科学史上有无数的事例可以证明,恩格斯的这种论断是十分正确的。事实上,岂只是高等数学的命题在刚提出的时候,常常被初等数学的代表人物看成是完全胡说八道的呢?还有其他许多科学的命题,当它们刚提出的时候,难道不也是被人看成完全胡说八道的吗?
事实上,当着人们只有初等数学知识的时候,就只能够对静止的固定的常数进行计算,以表明客观事物的量的关系;到了高等数学出现的时候,人们就进一步能够对发展运动中的变数进行计算,以表明客观事物的质的关系。由于初等数学受了机械论的形而上学的观点的支配,缺乏唯物辩证的观点,因此只有初等数学知识的人,无论如何不可能正确地理解事物的辩证关系。比如,对于曲线和直线的关系,在初等数学的代表人物看来是绝对不同的两个概念,却没有想到曲线的无限延伸的结果,就转化成为直线了。所以在高等数学的微分中,曲线和直线则是可以相等的。这样,在初等数学的代表人物的心目中,高等数学的许多命题,当然就成为完全胡说八道的命题了。
同样的例子在其他许多学科中,也都可以遇到不少。比如,动物学家最初对于鸭嘴兽就不知道应该怎样做正确的分类。因为按照归纳法进行动物分类的结果,凡是雌性有乳房的动物都是哺乳类的动物,反之,凡是雌性没有乳房的动物就都不是哺乳类的。按照这个标准来看鸭嘴兽,当然就不是哺乳类动物了。因为雌性的鸭嘴兽是没有乳房的。然而,事实证明鸭嘴兽却完全是哺乳类的动物。因此,恩格斯也指出,按照归纳法进行动物分类的结果,必然会造成错误。
由此可见,任何科学的结论都不应该被看成是永恒不变的,而任何新的科学论断的提出,只要言之成理,持之有故,也都不应该被看成是胡说八道的。因为人们对于客观规律,常常要经过多次反复才能认识清楚。科学研究的命题和结论不过是表示人们对于客观规律的一种认识阶段。昨天认为正确的结论,到了明天,由于新的事实证明,可能会发现并不完全正确,这时候,又需要对原来的结论做某些修改和补充,或者提出新的结论。只有这样,人的认识才能不断发展和提高,科学研究才能更好地掌握客观规律,来为人类服务。
为了使科学研究工作富有成果,我们完全应该鼓励年轻人大胆钻研,解放思想,敢想敢说敢干,决不要去泼他们的冷水,泄他们的气。我们要积极启发年轻的科学技术工作者和理论工作者,脚踏实地,虚心谨慎地向科学的高峰稳步前进。应该勉励大家既不要轻浮急躁,也不要因为怕被批评为胡说八道而放弃自己的雄心壮志。相反的,任何人只要在扎扎实实的研究基础上,如果真有新的发现,就要敢于提出所谓胡说八道的新的命题,而不必有任何顾虑。
木下 国夫・藤井義則 校正
燕山夜話 第2集18話(通算48話)“胡说八道”的命题
